Fallthrough Sort: Quickly Sorting Small Sets
In many applications, such as a median filter, we want to sort a small () set of numbers. In the case of the median filter, we are only concerned with sorting sets of one exact size – if this is the case, one can generate an optimal sorting network using a tool like this one to create a provably-unbeatable solution.
However, often we want to be able to sort sets of varying size that are still small. Perhaps if one wished to implement a 3x3, 5x5, and 7x7 median filter using a single sorting function. Or perhaps when sorting an arbitrary list of files, when there could be very many or very few items.
In this case, we can utilize a special implementation of bubble sort that takes advantage of switch statement fallthrough. To quickly sort sets of size , we could use this C code:
#include <stdlib.h>
#define min(a, b) (a < b ? a : b)
#define max(a, b) (a > b ? a : b)
#define exch(a, b) temp = a; a = min(temp, b); b = max(temp, b);
#define exch3(a, b, c) exch(a, b); exch(b, c);
#define exch4(a,b,c,d) exch3(a,b,c); exch(c,d);
#define exch5(a,b,c,d,e) exch4(a,b,c,d); exch(d,e);
#define exch6(a,b,c,d,e,f) exch5(a,b,c,d,e); exch(e,f);
#define exch7(a,b,c,d,e,f,g) exch6(a,b,c,d,e,f); exch(f,g);
#define exch8(a,b,c,d,e,f,g,h) exch7(a,b,c,d,e,f,g); exch(g,h);
#define exch9(a,b,c,d,e,f,g,h,i) exch8(a,b,c,d,e,f,g,h); exch(h,i);
int cmpfunc (const void * a, const void * b) {
return ( *(int*)a - *(int*)b );
}
// quickly sort an array if size is less than or equal to 9, otherwise use
// stdlib's qsort to sort the array.
void fallthroughSort(int* array, int length) {
int temp;
switch (length) {
case 9:
exch9( array[0],array[1],array[2],array[3],array[4],
array[5],array[6],array[7],array[8] );
case 8:
exch8( array[0],array[1],array[2],array[3],array[4],
array[5],array[6],array[7] );
case 7:
exch7( array[0],array[1],array[2],array[3],array[4],
array[5],array[6] );
case 6:
exch6( array[0],array[1],array[2],array[3],array[4],
array[5] );
case 5:
exch5( array[0],array[1],array[2],array[3],array[4] );
case 4:
exch4( array[0],array[1],array[2],array[3] );
case 3:
exch3( array[0],array[1],array[2] );
case 2:
exch(array[0], array[1]);
break;
default:
qsort(array, length, sizeof(int), cmpfunc);
}
}Each call to represents a bubble sort pass from index to index . Any array that is of size will jump to the proper pass of bubble sort, and execute all the required passes by falling through the switch statement.
You might be skeptical as to how a algorithm is outperforming a algorithm, but remember that big-O notation only defines asymptotic behavior. It is often the case that the actual performance of an algorithm depends on the constants hidden by big-O notation, as has been exhaustively discussed.
Of course, code similar to that above can be generated for any size, and a Python script to do just that is available in this BitBucket repository. We’ll take a look at the performance of this algorithm.
The following graph shows the performance of fallthrough sort (for ) compared to the standard library’s qsort function. Both functions sorted randomly generated lists of size .
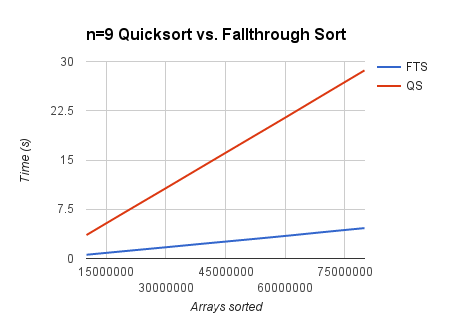
As you can see, fallthrough sort provides a substantial speed boost. Obviously, the difference is negligible if you’re only sorting one list.
This next graph shows the performance of fallthrough sort (for ) compared to the standard library’s qsort function when sorting lists of varying sizes.
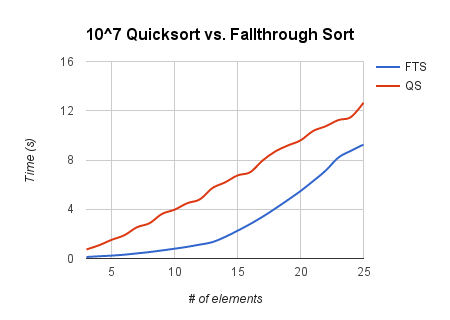
As the number of elements increases, fallthrough sort seems to slow down and approach the speed of qsort (eventually, qsort will become faster). This is expected, given the asymptotic behavior of each algorithm.
This last graph shows how many times faster fallthrough sort is compared to qsort.
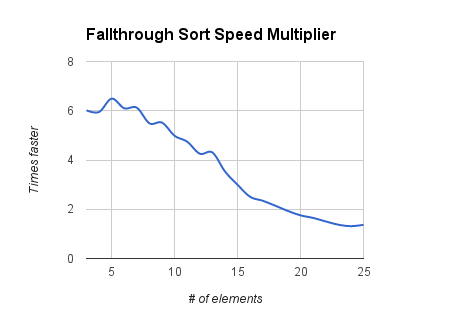
Here, the asymptotic behavior of both algorithms is extremely clear: qsort scales much better than fallthrough sort.
One might consider this comparison unfair because qsort evaluates a user-supplied comparison function. However, looking at the output of GCC reveals that when a very standard function (like the one above) is used, the comparison function is inlined.
One might also consider creating a branch table to jump right to the required pass of bubble sort. Once again, looking at optimized GCC output will show that the above switch statement is optimized into a branch table.
You can view a sample implementation and benchmark code over at BitBucket.
Reddit user sltkr seems to be getting better results from a simple insertion sort. This appears to be due to CPU differences, but the discussion is ongoing.