rdtheory.js: relational database algorithms in JavaScript

While reviewing my database theory textbook, I stumbled across a few algorithms for relational schema decomposition and database normalization. Aside from a dead project on Google Code and a buggy and apparently closed-source implementation hosted at the University of Illinois, I couldn’t really find any implementations or libraries implementing these algorithms.

So, I created rdtheory.js and a small 3NF decomposition tool. Neither are particularly polished or documented, but the library itself contains several tests. It is entirely synchronous, which could be a problem for very large schemes. At some point I might rewrite it with promises.

There are a few examples on the GitHub page, but working through an example might be useful. Consider a relation with the following attributes:

• First name
• Last name
• Email address
• Home address
• ZIP Code
• Manager
• Years with company
• Pay

We can represent this relation as :

Next, let’s consider the semantics of the information stored in . In order to do so, it is helpful to remember the definition of a functional dependency. We say that the set of attributes functionally depends on another set of attributes if and only if every pair of rows in that match on the attributes also match on the attributes . In other words, if and , then we would say that one’s ZIP code functionally depends on one’s home address if and only if any two individuals with the same home address also have the same ZIP code. We write this functional dependency as . We can also say that determines .

For our example, let’s assume the following set of functional dependencies:

An employee’s first and last name determines their email address:

An employee’s first and last name determines their home address:

An employee’s home address determines their ZIP code:

An employee’s email address determines their manager:

An employee’s years of service and their manager determines their pay:

Now, as database programmers, we could simply create one table with each attribute in as a column. But we know better! With our relation and all these functional dependencies, we can use various algorithms and theorems from relational algebra to create a 3NF decomposition.

Using the tool I developed, we can decompose without computing minimal covers ourselves.

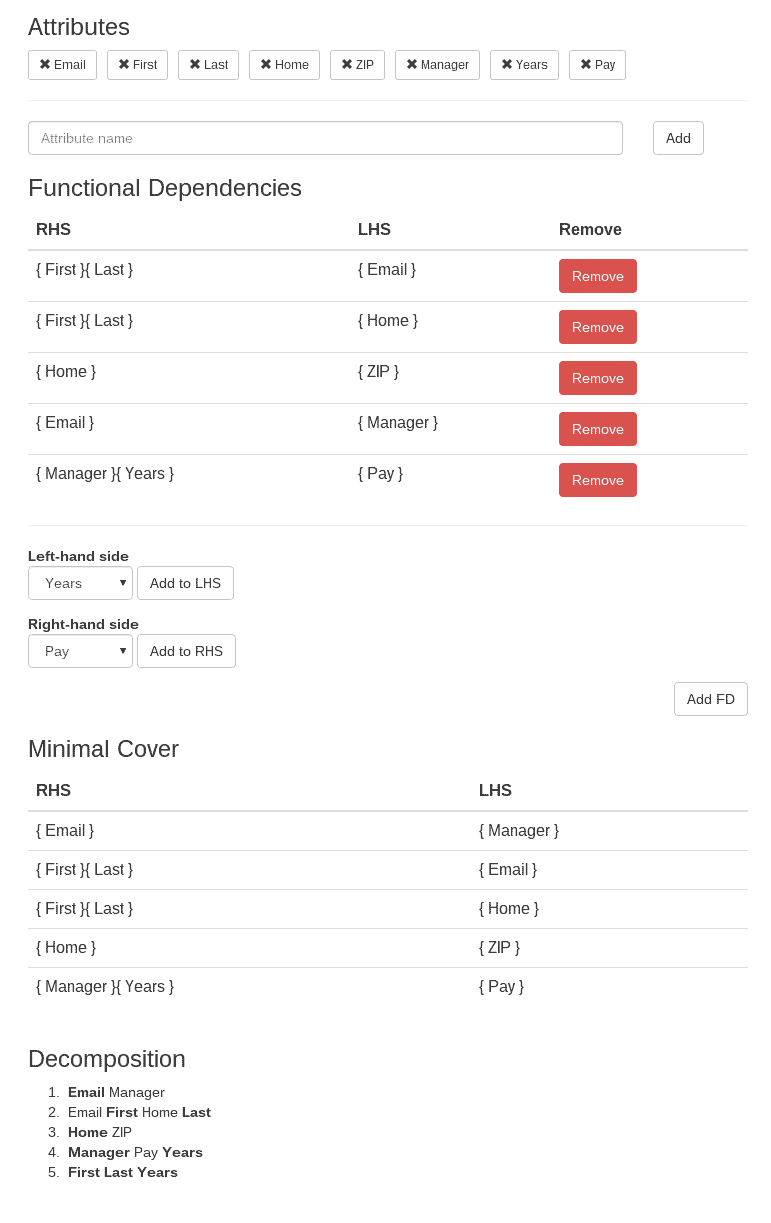
From the tool, we can see that our universal relation was not in 3NF. The tool suggests a decomposition of into five relations, and conveniently marks the keys of each new relation with boldface. We can formally represent this decomposition as:

Now, we can create five tables instead of one. The algorithm used also ensures that the decomposition preserves all dependencies and is a loseless join decomposition.

Happy normalizing!