A JavaScript Connect Four AI

Might I interest you in a rousing game of Connect Four? You and the computer take turns dropping discs into one of the seven colums below. The goal is to get four pieces of your color in a row (vertically, diagonally, or horizontally).

Winner: none yet...Player {{winner}}

Draw: noyes

Moves to to think ahead

That’s an AngularJS powered Connect Four AI that was originally written in C and then compiled to JavaScript using Emscripten. It runs the actual AI in a web worker to prevent your browser from locking up.

It was implemented using techniques from Stuart Russell and Peter Norvig’s excellent book, Artificial Intelligence: A Modern Approach (3rd Edition). These techniques might not create the best Connect Four AI possible (in fact, Victor Allis’ thesis shows how to create a provably-unbeatable AI), but it can still do pretty well! The code (in C, Python, and JavaScript) is available on GitHub.

The main idea behind the AI is adversarial search. Think of all the possible games of Connect Four represented as a tree. The root of the tree is the empty board. The second tier of the tree represents all the possible moves that can be made by the first player. The third tier of the tree represents all the possible moves that can be made by the second player.

A small subset of the tree (for a small game board) might look like this:

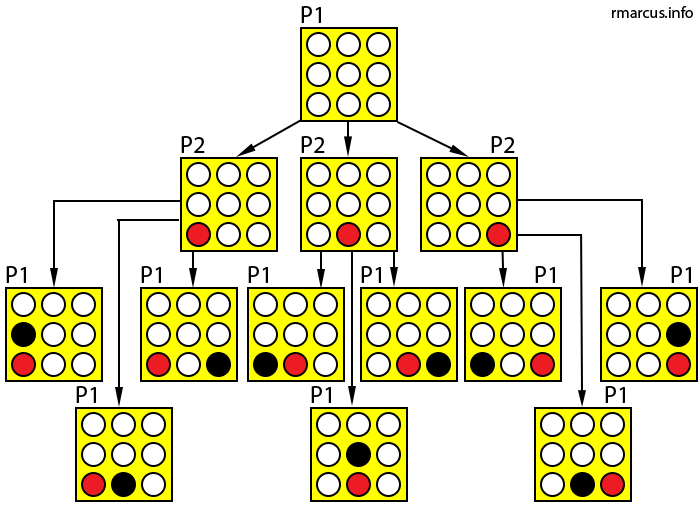
Imagine expanding the tree all the way down to the bottom, where the leaf nodes are “terminal” states – states where one player has won the game, or there is a draw. In order to make moves, the AI applies a minimax strategy. In other words, the AI assumes that its opponent will always play optimally, and thus tries to minimize the maximum gain of its opponent.

This tree is really big. The branching factor is approximately seven, and the depth of the tree could be as high as 42. So, while the the perfect tree formula would tell us that there are boards, some smart mathematicians have figured out that there are “only” around 4 trillion different boards. That’s still way too many to examine.

Thankfully, we can use a technique called alpha-beta pruning. The idea is pretty simple: do not bother searching branches that would either:

• require our opponent to make a detrimental move (to get an outcome less than the outcome they could get if they played optimally)
• or, require us to make a move that was less advantageous than another move we could make

Now, this is a hand wavey oversimplification of how the process actually works. I suggest you read the chapters in Russell and Norvig, or fuss through the Wikipedia page, to get a better understanding.

In the average case, alpha-beta pruning reduces the number of nodes we need to evaluate from to . This brings us from 4 trillion boards to around 2.7 billion boards. A pretty good drop – but still not enough for us to enumerate.

Next, we employ a heuristic function. Since we can’t reach the bottom of the tree, we’ll go down a certain depth and then make some kind of guess as to whether or not the board we are evaluating is a winning or losing board. I used a very simple heuristic: the number of possible four-in-a-rows. The computer would calculate how many ways it could win using alignments present in the current board, and then subtract the number of ways the computer’s opponent could win.

Now, the computer will exhaustively evaluate the tree to a certain depth (the number of moves to “think ahead”) and then use a heuristic to evaluate that board. Eventually, as the end of the game draws near, the computer finds winning or losing states within the prescribed depth, and plays perfectly. The hope is that the heuristic function can guide the AI to a winnable position. It seems to work pretty well – if you can beat it, try increasing the number of moves to think ahead. It’ll make it slow down, but it’ll get exponentially more difficult.

Oh – there’s one more complication. A lot of the boards that you encounter when going down the tree are duplicates (there is more than one way to get to a state). To avoid recomputing the desirability of these boards, we store them in a hash table.

It also looks like writing this type of AI is homework for AI classes at Cornell, Northeastern, and Purdue. I could only find one other Javascript Connect Four AI, which moves substantially faster than mine, but is easily defeated (which is exactly the behavior one would expect).