Machine learning for systems
Imagine you are writing a system to repeatedly sort large datasets. You could just blindly choose a search algorithm, like Quicksort, and apply it every time. However, if the data is nearly sorted already, something like bubble sort or insertion sort might be a better idea. But how do we know when this is the case? One approach would be to sample the data and compute some statistics over it, like the expected size of a run1 and the average pairwise difference. Then, you could run a lot of experiments and try to come up with a hand-tuned heuristic to pick a sorting algorithm based on the sampled information.
But how well will the heuristic you designed work when the data distribution changes? Or when your system is moved to new hardware (possibly with larger caches, etc.)? Or you want to add some other sorting algorithm? Some of the thresholds you picked might need to be tuned… every single time.
So why don’t we just learn the function that maps our sampled statistics to the optimal sorting algorithm? And better yet, let’s do it in an online fashion, using a corrective feedback loop where we learn from our mistakes.
| State | |
|---|---|
| Quicksort | |
| Insertion | |
| Bubble | |
ExperienceThe total number of sorts the agent has performed, and thus the amount of training data acquired, so far. |
|
Net regretThe time difference between the action taken by the policy (the agent or Quicksort, QS) and the optimal action over every episode so far. |
Agent: / QS: |
Net savingsThe amount of time saved (if positive) or lost (if negative) by using the learning agent instead of picking Quicksort every time. |
Right now, your computer is busily training and evaluating a deep reinforcement learning model2 which, when fed the sampled statistics as input, will predict how long each of three sorting algorithms (Quicksort, bubble sort, and insertion sort) will take to sort the data. The graph shows the regret, the difference between the decision made and the optimal decision, for two policies: the learned model, and a policy that uses Quicksort every time. The “net savings” measures how much time has been saved (or lost) by using the learned policy compared to Quicksort. Over time, this number should increase, indicating that the agent is learning.
What’s going on here?
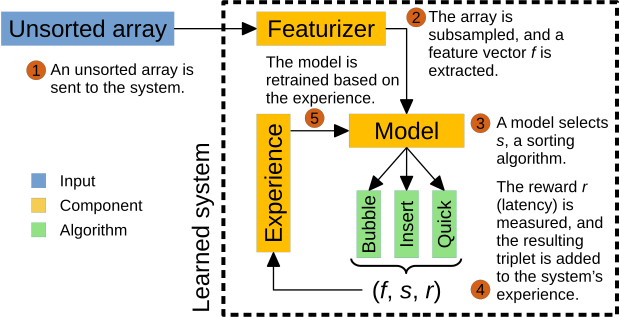
Every time a new set arrives for sorting (an episode), we feed the sampled statistics (the context) to the neural network, and we use the network’s prediction to select a sorting algorithm (an action). After we select an algorithm, we sort the set and see how good our decision was by measuring the latency (the reward). This problem setup, a restriction of general reinforcement learning, is often referred to as the contextual multi-armed bandit problem3, in which:
- At the start of each episode, an agent receives a context (sampled statistics), containing information relevant to the current episode.
- The agent selects an action (a sorting algorithm) from a finite set.
- The agent receives some reward (the time it takes to sort).
The agent’s goal is to maximize the reward it earns over time (i.e., minimize the latency of sorts over time). In order to do so, the agent must explore the relationship between contexts, actions, and rewards, while simultaneously exploiting the knowledge it has gathered. Our solution to this problem is Thompson sampling, a straight-forward technique that keeps track of (context, action, reward) triples and samples a model to predict the reward of each action based on the context.
We re-train the model every 40 episodes. As the model gains more and more experience (observed triples), the model’s prediction gets better and better, and thus the resulting policy improves as well.
If you watch the graph for long enough (normally around 250 episodes), the regret of the learned policy should go to zero, meaning that the optimal policy has been learned. Since we use Thompson sampling to build a new model every 40 episodes, there are occassionally spikes, or variance, in the learned model’s policy. However, the net savings of the learned model tends to remain significant.
In a sense, this means our learned model is trading worst-case performance for average-case performance: most of the time, the learned model will choose a good algorithm, but every once in a while, Thompson sampling will produce a catestrophic policy,4 and performance will degrade significantly for a short period of time. But, on average, the learned agent will perform better than the static policy.
The Big Picture
Machine learning for systems – that is, applying machine learning techniques to problems within computer systems – is coming, and it’s coming fast. Whether its index structures, scheduling, or even database query optimization (including cardinality estimation), machine learning is creeping its way into the domain of systems. It has been called Software-Defined Software, Software 2.0, learned systems components, or self-assembling systems. But regardless of the name, “machine learning for systems” brings about both exciting possibilities and significant new challenges.
The advantages of machine learning powered systems could be huge: for database systems, query optimizers contain a huge number of heuristics that must be painstakingly maintained by hand, and often even require application-specific tuning by a DBA. Some of our recent research shows how deep reinforcement learning can produce query optimizers that automatically tune themselves to specific applications, matching and sometimes exceeding the performance of complex commercial optimizers. In their recent paper, Kraska et al. argue that similar applications of machine learning could improve almost every aspect of a database, including data access, query optimization, query execution, and advanced analytics.
However, there are numerous challenges to overcome.
-
Like in the example shown here, learned systems can perform better on average, but might have significantly higher variance, especially in early episodes. Figuring out how to reduce this variation will be critical for systems applications that depend on low tail latencies. Several approaches, like learning from demonstration or bootstrapping a model from a cost function, have recently been investigated.
-
Understanding when models will – and won’t – work is still a major open question. While we know that neural networks can approximate any continuous function, and that algorithms like table-based Q learning converge to optimal policies for any MDP, we are still a long way from having theoretically-justified bounds on practical learning systems. It is possible that such bounds may never be known, and that it is easier to adjust the existing learning systems to have better behavior at the margins. Such techniques could be a simple as using different models for outliers, or may be as complex as modifying database internals to work adaptively.
-
Doing worse takes longer than doing well. If you are playing a video game and not doing very well, the score printout on the screen will tell you just how bad you doing. If you are doing well, the score printout will convey this information as well, and equally quickly. For systems problems, however, if your initial policy is poor, evaluating it may take a long time. For example, for join order selection in a relational database, a bad join ordering may take orders of magnitude longer to complete than a good one. Thus, how long it takes to “read the score” is a function of the score itself. This means that the initial episodes of learning (in which many RL algorithms start with a random policy) could take a prohibitively long amount of time.
These challenges, and many others, are discussed in our recent workshop paper at RL4RealLife (ICML ‘19). We’ve also released an open source platform called Park to enable researchers to test reinforcement learning algorithms on systems problems, including network congestion control, Spark scheduling, load balancing, and a dozen more. The future of systems is learned!
FAQs
This seems really dumb. Why don’t you just… This is not supposed to be a practical system. It’s supposed to be a demonstration of a learned policy being useful in a systems context. Clearly, a real world system would need significantly more testing, and would likely use a much simpler model. Please see the many linked works in the first paragraph of “The Big Picture” section for more practical examples.
Are you including the featurization and inference time in your measurement? Inference time is not included, but featurization time is included: the always-quicksort policy benefits from not having to compute features, and the learned policy is punished. Note that the zero-regret line on the plot assumes the featurization times – in other words, an oracle policy that didn’t even require the features as inputs would have a (slightly negative) regret.
Shouldn’t you just be using Timsort? Maybe. Depends on the hardware, data distribution… probably a large number of other factors. This system is flexible – you could add in Timsort, and, if a particular piece of hardware and data distribution caused Timsort to always be optimal, Timsort would always be selected. In this case, you would be wasting time computing features. It might be interesting to have the policy select which features it wanted to gather for itself, so that the network could learn which when/which features were useful.
-
A run is a contiguous sorted subsequence, i.e., a cluster of data that is already sorted within the larger dataset. ↩
-
With just two inputs and one output, we could’ve easily (and, if this were a real system, should’ve!) used something simpler, like a decision tree. But what fun would that be? ↩
-
There are many overviews available. For one, see: Chapelle and Li. “An Empirical Evaluation of Thompson Sampling.” In Advances in Neural Information Processing Systems. NIPS’11. ↩
-
Testing these catastrophic policies is a necessary part of most reinforcement learning – after all, if we do not test the policy, how will we ever learn it is catastrophic? We don’t want the performance of real world systems to suffer while our models explores no-good possibilities. Figuring out how to avoid such catastrophic detours is an active area of research. ↩